Constrained Fitting¶
This example shows how to fit a \({\Delta\chi}\)-tensor with constraints applied. The two cases here constrain position to fit a tensor to a known metal ion position form an X-ray structure, and fit an axially symmetric tensor with only 6 of the usual 8 parameters.
Downloads¶
Download the data files
4icbH_mut.pdbandcalbindin_Er_HN_PCS.npcfrom here:Download the script
pcs_fit_constrained.py
Script + Explanation¶
The necessary modules are imported and data is loaded
from paramagpy import protein, fit, dataparse, metal
# Load data
prot = protein.load_pdb('../data_files/4icbH_mut.pdb')
rawData = dataparse.read_pcs('../data_files/calbindin_Er_HN_PCS.npc')
parsedData = prot.parse(rawData)
mStart = metal.Metal()
The calcium ion from the X-ray structure is contained in a heteroatom of the PDB file. We set the starting position of the tensor to this position.
# Set the starting position to Calcium ion heteroatom in PDB
mStart.position = prot[0]['A'][('H_ CA', 77, ' ')]['CA'].position
To fit the the anisotropy and orientation without position, the linear PCS equation can be solved analytically by the SVD gridsearch method but using only one point with a radius of zero. The Q-factor is then calculated and the tensor is saved.
# Calculate tensor by SVD
[mFit], [data] = fit.svd_gridsearch_fit_metal_from_pcs(
[mStart],[parsedData], radius=0, points=1)
qfac = fit.qfactor(data)
mFit.save('calbindin_Er_HN_PCS_tensor_position_constrained.txt')
Output: [pcs_fit_constrained.png]
ax | 1E-32 m^3 : -8.152
rh | 1E-32 m^3 : -4.911
x | 1E-10 m : 25.786
y | 1E-10 m : 9.515
z | 1E-10 m : 6.558
a | deg : 125.841
b | deg : 142.287
g | deg : 41.758
mueff | Bm : 0.000
shift | ppm : 0.000
B0 | T : 18.790
temp | K : 298.150
t1e | ps : 0.000
taur | ns : 0.000
To fit an axially symmetric tensor, we can used the Non-linear regression method and specify exactly which parameters we want to fit. This will be the axiality ax, two Euler angles b and g and the position coordinates. Note that in the output, the rhombic rh and alpha a parameters are redundant.
# Calculate axially symmetric tensor by NRL
[mFitAx], [dataAx] = fit.nlr_fit_metal_from_pcs(
[mStart], [parsedData], params=('ax','b','g','x','y','z'))
qfacAx = fit.qfactor(dataAx)
mFitAx.save('calbindin_Er_HN_PCS_tensor_axially_symmetric.txt')
Output: [pcs_fit_constrained.png]
ax | 1E-32 m^3 : 9.510
rh | 1E-32 m^3 : 0.000
x | 1E-10 m : 24.948
y | 1E-10 m : 8.992
z | 1E-10 m : 3.205
a | deg : 0.000
b | deg : 134.697
g | deg : 180.000
mueff | Bm : 0.000
shift | ppm : 0.000
B0 | T : 18.790
temp | K : 298.150
t1e | ps : 0.000
taur | ns : 0.000
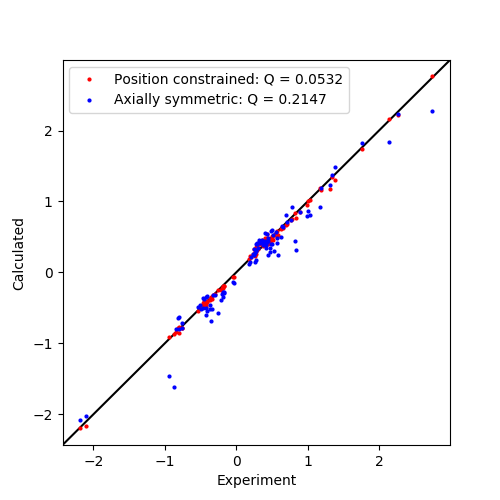
Finally we plot the data.
#### Plot the correlation ####
from matplotlib import pyplot as plt
fig, ax = plt.subplots(figsize=(5,5))
# Plot the data
ax.plot(data['exp'], data['cal'], marker='o', lw=0, ms=2, c='r',
label="Position constrained: Q = {:5.4f}".format(qfac))
ax.plot(dataAx['exp'], dataAx['cal'], marker='o', lw=0, ms=2, c='b',
label="Axially symmetric: Q = {:5.4f}".format(qfacAx))
# Plot a diagonal
l, h = ax.get_xlim()
ax.plot([l,h],[l,h],'-k',zorder=0)
ax.set_xlim(l,h)
ax.set_ylim(l,h)
# Make axis labels and save figure
ax.set_xlabel("Experiment")
ax.set_ylabel("Calculated")
ax.legend()
fig.savefig("pcs_fit_constrained.png")
Output: [pcs_fit_constrained.png]