Propagate Uncertainty to Fitted Tensor Parameters

This example shows the various error analysis functions available in paramagpy for estimating the unceratinty in fitted parameters for a paramagnetic center.

Downloads

• Download the data files 2bcb.pdb and calbindin_Er_HN_PCS_errors.npc from here:

• Download the script pcs_fit_uncertainty.py

Script + Explanation

This start of this script follows the script Fit Tensor to PCS Data to fit the tensor.

from paramagpy import protein, fit, dataparse, metal
import numpy as np

# Load the PDB file
prot = protein.load_pdb('../data_files/2bcb.pdb')

# Load the PCS data
rawData = dataparse.read_pcs('../data_files/calbindin_Er_HN_PCS_errors.npc')

# Associate PCS data with atoms of the PDB
parsedData = prot.parse(rawData)

# Define an initial tensor
mStart = metal.Metal()

# Set the starting position to an atom close to the metal
mStart.position = prot[0]['A'][56]['CA'].position

# Calculate an initial tensor from an SVD gridsearch
[mGuess], [data] = fit.svd_gridsearch_fit_metal_from_pcs(
	[mStart],[parsedData], radius=10, points=10)

# Refine the tensor using non-linear regression
[mFit], [data] = fit.nlr_fit_metal_from_pcs([mGuess], [parsedData])

Uncertainty from structure models

The PDB file contains models that capture uncertainty in the structure of the protein. This can be propagated to estimate uncertainty in the fitted tensor parameters using the fnction paramagpy.fit.fit_error_model(). This fits a separate tensor to each model and returns all fitted tensors as well as the standard deviation in the fitted parameters.

# Estimate uncertainty sourcing noise from the models of the PDB
[mod_all], [mod_std] = fit.fit_error_models(fit.nlr_fit_metal_from_pcs, 
	initMetals=[mFit], dataArrays=[parsedData])

mod_std.save('error_tensor_models.txt')

The standard deviation in the fitted tensor parameters is found in the variable mod_std. This variation in tensor principle axes can be viewed by a Sanson-Flamsteed plot.

Output: [error_tensor_models.txt]

ax    | 1E-32 m^3 :     0.556
rh    | 1E-32 m^3 :     0.525
x     |   1E-10 m :     0.756
y     |   1E-10 m :     0.695
z     |   1E-10 m :     0.957
a     |       deg :     7.466
b     |       deg :     9.948
g     |       deg :    19.294
mueff |        Bm :     0.000
shift |       ppm :     0.000
B0    |         T :     0.000
temp  |         K :     0.000
t1e   |        ps :     0.000
taur  |        ns :     0.000

Output: [models.png]

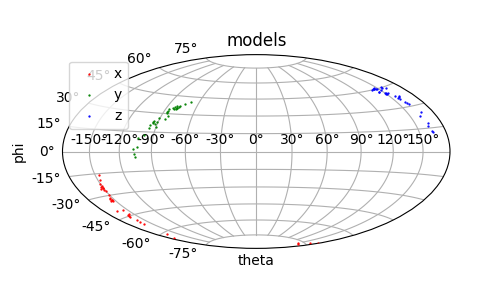
Uncertainty from experimental uncertainties

Experimental uncertainties can be measured. This may arise due to spectral noise in peak heights for PREs, or spectral noise as uncertainties in chemical shifts for PCSs, as is the case here. The function paramagpy.fit.fit_error_monte_carlo() will repeat the fit for many iterations, each time adding random noise from a uniform distribution scaled by the experimental errors present in the err column of the dataArray parsedData.

# Estimate uncertainty sourcing noise from experimental uncertainties
[mc_all], [mc_std] = fit.fit_error_monte_carlo(fit.nlr_fit_metal_from_pcs, 
	50, initMetals=[mFit], dataArrays=[parsedData])

mod_std.save('error_tensor_monte_carlo.txt')

Output: [error_tensor_monte_carlo.txt]

ax    | 1E-32 m^3 :     0.556
rh    | 1E-32 m^3 :     0.525
x     |   1E-10 m :     0.756
y     |   1E-10 m :     0.695
z     |   1E-10 m :     0.957
a     |       deg :     7.466
b     |       deg :     9.948
g     |       deg :    19.294
mueff |        Bm :     0.000
shift |       ppm :     0.000
B0    |         T :     0.000
temp  |         K :     0.000
t1e   |        ps :     0.000
taur  |        ns :     0.000

Output: [monte_carlo.png]

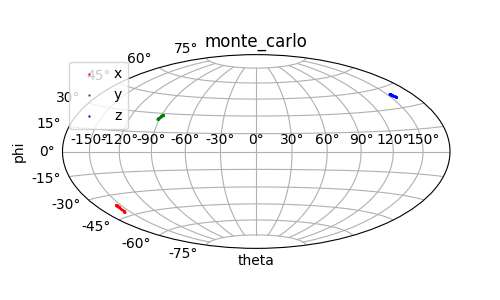
Uncertainty from sample fraction

A final, but generally not recommended method is to source noise from taking a random fraction of the data and conducting the fit for many iterations to then view the deviation in fitted parameters. This method is often called bootstrapping and is desirable if the experimental uncertainties are unknown and the PDB file does not contain models that capture structural unceratinty. The function paramagpy.fit.fit_error_bootstrap() will repeat the fit for many iterations, each time sampling the desired amount of the experimental data randomly.

# Estimate uncertainty sourcing noise from sample fractions
[bs_all], [bs_std] = fit.fit_error_bootstrap(fit.nlr_fit_metal_from_pcs, 
	50, 0.8, initMetals=[mFit], dataArrays=[parsedData])

mod_std.save('error_tensor_bootstrap.txt')

Output: [error_tensor_bootstrap.txt]

ax    | 1E-32 m^3 :     0.556
rh    | 1E-32 m^3 :     0.525
x     |   1E-10 m :     0.756
y     |   1E-10 m :     0.695
z     |   1E-10 m :     0.957
a     |       deg :     7.466
b     |       deg :     9.948
g     |       deg :    19.294
mueff |        Bm :     0.000
shift |       ppm :     0.000
B0    |         T :     0.000
temp  |         K :     0.000
t1e   |        ps :     0.000
taur  |        ns :     0.000

Output: [bootstrap.png]

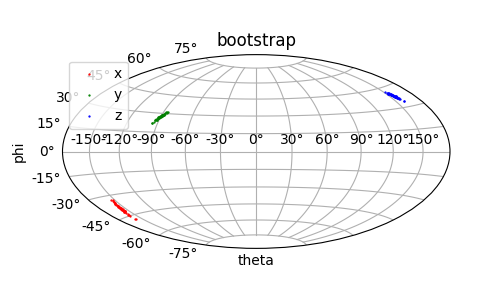
This piece of code is used to generate the Sanson-Flamsteed projection plots

#### Plot Sanson-Flamsteed ####
from matplotlib import pyplot as plt

def transform(vector):
	x, y, z = vector
	theta = np.arctan2(y, x)
	phi = -np.arccos(z) + np.pi/2.
	return theta, phi

for name, mset in [('models',mod_all), ('monte_carlo',mc_all), ('bootstrap',bs_all)]:
	spcoords = []
	for m in mset:
		x, y, z = m.rotationMatrix.T
		spcoords.append(tuple(map(transform, [x,y,z])))
	points = zip(*spcoords)
	fig = plt.figure(figsize=(5, 3), dpi=100)
	ax = fig.add_subplot(111, projection='hammer')
	ax.set_xlabel("theta")
	ax.set_ylabel("phi")
	ax.set_title(name)
	ax.grid()
	for data, col, label in zip(points, ['r','g','b'], ['x','y','z']):
		theta, phi = zip(*data)
		ax.scatter(theta, phi, s=0.4, c=col, label=label, zorder=10)
	ax.legend()
	fig.savefig("{}.png".format(name))